Architettura del cerchio

di Edmondo Jonghi Lavarini

L’epica battaglia fra 兀 e τ

Esplora la battaglia epica tra 兀 (pi greco) e τ (tau): una storia di scoperta, innovazione e rivincite matematiche. Scopri perché 兀 regna e come τ potrebbe cambiare il gioco.

La storia del 兀 (pi greco) e τ (tau) è affascinante e illustra come concetti matematici possano evolversi e competere nel tempo. Entrambi i numeri hanno un ruolo fondamentale nella matematica e nella comprensione delle proprietà dei cerchi, ma la loro “battaglia” è di natura più moderna e concettuale piuttosto che un confronto diretto tra matematici dell’antichità.

兀 (Pi Greco): Un Antico Gigante

La storia del 兀 inizia nell’antichità, quando civiltà come Egizi e Babilonesi cercavano di comprendere le proporzioni e le proprietà dei cerchi. Essi approssimavano 兀 con vari metodi, dando vita a stime che, seppur grezze, erano sorprendentemente vicine al vero valore. Ad esempio, il Papiro di Rhind (1650 a.C. circa) suggerisce che gli antichi Egizi usassero un valore di 兀 pari a circa 3,16, mentre i Babilonesi avevano una stima di circa 3,125.

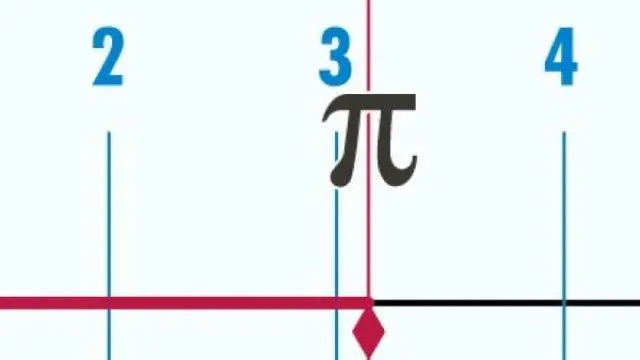
Nel linguaggio dell’architettura, il cerchio e Pi greco incarnano l’essenza dell’armonia, della completezza e dell’equilibrio. Attraverso la precisione di 兀, gli architetti delineano le proporzioni circolari, fondamentali per la progettazione di cupole, volte e archi, che sottolineano la continuità visiva e strutturale. Questi elementi, imbevuti di una profonda estetica e rigore scientifico, sono pilastri nella creazione di spazi che risuonano con la bellezza intrinseca 兀 del mondo naturale, manifestando l’intersezione tra forma, funzione e filosofia architettonica.

Più tardi, matematici greci come Archimede di Siracusa (287-212 a.C.) applicarono metodi geometrici per calcolare una stima più accurata del 兀 utilizzando poligoni inscritti e circoscritti per approssimare la circonferenza del cerchio. Archimede fu in grado di determinare che il valore del 兀 si trova tra 3,1408 e 3,1429, un risultato notevolmente preciso per il suo tempo.

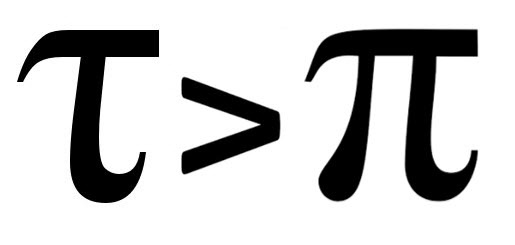
Che sia TAU o PI GRECO per il cerchio e le architetture circolari sono fondamentali in architettura, simboleggiando perfezione, unità e armonia. Attraverso queste costanti architetti calcolano circonferenze e aree, essenziali per strutture rotonde, cupole e archi. Questa conoscenza guida la creazione di spazi e strutture, unendo bellezza e scienza.

τ (Tau): Una Rivincita Moderna

Il numero τ, che equivale a 2兀 o circa 6,2832, è una proposta più recente nel panorama matematico. L’idea dietro τ è che esso possa essere un modo più intuitivo e diretto per descrivere le relazioni e le proprietà dei cerchi, soprattutto perché molte formule, come la lunghezza della circonferenza C = τr diventano più semplici.

Il Pi Greco è la base numeriche di tutte le geometrie che derivano dal cerchio

La “battaglia del Tau” è stata promossa principalmente da matematici e educatori del XXI secolo, come Michael Hartl, che nel 2010 ha proposto l’uso di τ per semplificare l’insegnamento e la comprensione della matematica circolare. Hartl e altri sostenitori di τ argomentano che, adottando τ al posto di 兀 si riduce la confusione e si migliorano le intuizioni matematiche, specialmente per gli studenti.

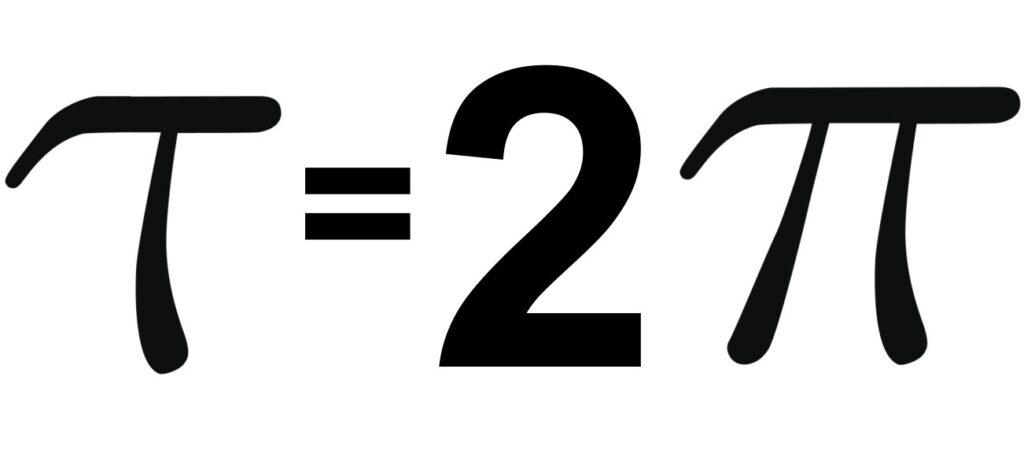
Perché il 兀 ha “Vinto”

Nonostante l’interesse crescente per τ , 兀 rimane il numero predominante per descrivere le relazioni circolari. Ciò è dovuto in gran parte alla sua lunga storia e alla profonda radicazione nella letteratura matematica, scientifica e educativa. Il 兀 è stato studiato e utilizzato per millenni; la sua presenza è onnipresente in innumerevoli formule, dalla geometria all’analisi, alla fisica.

*Leon Battista Alberti*
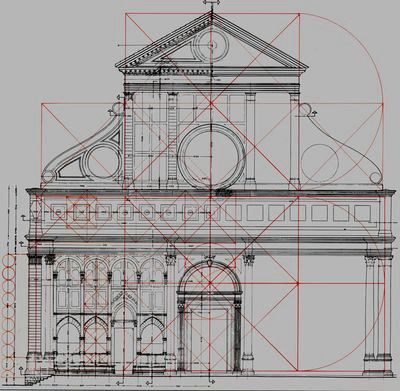
**Santa Maria Novella**, 1456
Firenze: Che sia TAU o PI GRECO sono entrambi fondamentali in architettura, simboleggiando perfezione, unità e armonia. Attraverso queste costanti universali, da secoli, gli architetti calcolano circonferenze e aree, essenziali per strutture rotonde, cupole e archi. Questa conoscenza guida la creazione di spazi, volumi e strutture solide, che uniscono bellezza e scienza.

La Potenziale Rivincita del τ TAU

Tuttavia, il dibattito tra 兀 e τ riflette una dinamica viva e in evoluzione nella matematica, dove le convenzioni possono essere sfidate e nuove idee possono emergere per migliorare la comprensione e l’applicazione dei concetti matematici. Mentre 兀 continua a dominare per motivi storici e convenzionali, l’interesse per τ evidenzia un desiderio costante di esplorare approcci che potrebbero rendere la matematica più accessibile e intuitiva.

In un’epoca dominata dalla tecnologia, c’è un fascino ineguagliabile nel ritorno alle origini della geometria, giocando con il compasso per esplorare le geometrie circolari. Questo semplice strumento, abbinato alla saggezza millenaria del cerchio, invita a riscoprire il piacere autentico della creazione manuale. Vi è una sottile magia nell’utilizzare il compasso per tracciare perfette circonferenze, un promemoria che, nonostante l’avanzare delle tecnologie, alcune verità fondamentali restano incantevolmente semplici. Così, mentre abbracciamo il futuro, non dimentichiamo di valorizzare e divertirci con gli strumenti e i concetti che hanno plasmato la nostra comprensione del mondo.

La “vittoria” del 兀 è quindi non tanto una questione di superiorità intrinseca, quanto piuttosto di radicamento storico e ampio utilizzo. La possibile “rivincita” di τ, d’altra parte, risiederebbe nella sua capacità di promuovere una comprensione più diretta e intuitiva delle proprietà dei cerchi e delle relazioni circolari. La proposta di τ come alternativa a 兀 non mira a sostituire completamente il 兀 ma piuttosto a offrire un’opzione che potrebbe semplificare alcune aree della matematica e dell’istruzione matematica.

L’adozione di τ potrebbe aumentare se la comunità matematica e educativa riconoscessero ampiamente i suoi vantaggi nell’insegnamento e nell’applicazione pratica, soprattutto nelle discipline che riguardano la circonferenza e le proprietà dei cerchi. Questo cambiamento richiederebbe, tuttavia, un significativo aggiustamento nei materiali didattici, nei libri di testo e nella pratica matematica consolidata.

L’interesse per τ evidenzia anche un aspetto più ampio della matematica: la disciplina non è statica, ma si evolve in risposta a nuove scoperte, idee e approcci pedagogici. La “battaglia” tra 兀 e τ è un esempio di come i matematici continuano a riflettere su e valutare le convenzioni, cercando modi per migliorare la comprensione e l’applicazione dei concetti matematici.

In conclusione, mentre 兀 mantiene la sua posizione preminente grazie alla sua storica onnipresenza e significato culturale, il dibattito su τ sottolinea l’importanza dell’innovazione e della riflessione critica nella matematica. La possibilità che τ possa “riprendersi la rivincita” dipenderà dalla sua accettazione da parte della comunità matematica e dall’efficacia con cui può migliorare l’insegnamento e la comprensione dei concetti circolari. La storia di 兀 e τ illustra bellamente come la matematica sia un campo vivo, caratterizzato da un costante scambio di idee e dalla ricerca di maggiore chiarezza e comprensione.